23 Two-Factor ANOVAs
Jenna Lehmann
So far we’ve talked about tests which are used if there is one independent variable, either with two levels or more. This is not the limit of how much we can include in a single analysis. In a two-factor ANOVA, there is more than one independent variable and each of those variables can have two or more levels. Take this example into consideration:
A farmer wants to know the best combination of products to use to maximize her crop yield. She decides to test out three different fertilizer brands (A, B, and C) and two different kinds of seeds (Y and Z). Each product is paired once with another for a total of 6 conditions: AY, BY, CY, AZ, BZ, CZ.
A two-factor ANOVA considers more than one factor and considers the joint impact of factors. This means that instead of running a new study every time you want to see how an independent variable affects a specific dependent variable, you can run an experiment with two different independent variables and seeing how they each impact the dependent variable and you get to see if the two independent variables do anything together to affect the dependent variable. These are called main effects and interactions. Keeping the example going, if we find that no matter what the seed type is that fertilizers A, B, and C resulted in different crop yields from one another, we would say there is a main effect for fertilizer type. If no matter what the fertilizer type is there is a difference between the crop yields of seeds Y and Z, we would say that there is a main effect for seed type. If there are times that the two factors influence each other (for example, let’s say that fertilizer worked much better specifically when paired with Y seeds), we would say there’s an interaction. The defining characteristic of an interaction is when the effect of one factor depends on the different levels of a second factor or the impact of another factor, either amplifying or reducing the effect based on the level.
Meaning of the Equation Before the ANOVA
Often times when reading a paper which uses a multiple factor ANOVA, there is a little equation before it like 2×2 or 4x5x2 or something along those lines. These equations may look confusing and intimidating, but there is a simple way to read these. The number of numbers in the equation tells you how many factors there are. For instance, a 2×3 ANOVA simply has two factors because there are only two numbers presented. A 4x5x7x2x3x4 ANOVA, although this equation looks ridiculous, simply has six factors in it because there are six numbers present. The actual values of each number tell you how many levels are in each factor. A lot of papers make sure to define which factors they’re considering first, but simply put, a 2×3 ANOVA has two factors and the first factor has two levels while the second has three. A 4x5x7x2x3x4 ANOVA has six factors, the first has four levels, the second has five, the third has seven, the fourth has two, the fifth has three, and the sixth has four. This author has personally never come across an ANOVA so convoluted in a paper, but this example was just meant to show that although it’s easy to get caught up in the sheer volume of numbers, interpreting them is not so complicated. Also remember that it’s the author’s job in an article to interpret the results for you, so that should help.
Hypothesis Testing with Two-Factor ANOVAs
For an ANOVA with only two factors (which is all you’ll likely need to master), there are three different null and alternative hypotheses to consider. One is for the first main effect, one is for the second main effect, and one is for an interaction. Don’t forget to include as many means as there are levels.
Null:
![]()
![]()
H0: There is not an A X B interaction
Alternative:
![]()
![]()
H1: There is an A X B interaction
The following are the steps and stages needed to calculate a two-factor ANOVA. Please keep in mind that the formulas needed for these calculations exist in the statistics formula glossary post.
- First Stage:
- Is identical to independent samples ANOVA
- Compute the
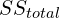 ,
, 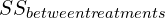 , and
, and 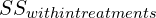
- Second Stage:
- Calculate
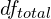 ,
, 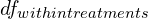 ,
, 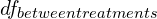 ,
, 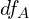 ,
, 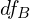 , and
, and 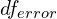 .
.
- Calculate
- Third Stage:
- The goal is to partition the
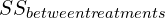 into three separate components
into three separate components - Calculate
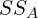 ,
, 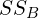 , and
, and 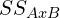 . In other words, calculate the parts of
. In other words, calculate the parts of 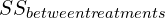 which can be attributed to main effect one, main effect two, and an interaction.
which can be attributed to main effect one, main effect two, and an interaction.
- The goal is to partition the
- Fourth Stage:
- Calculate
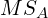 ,
, 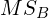 ,
, 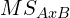 , and
, and 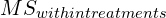 .
.
- Calculate
- Fifth Stage:
- Calculate
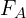 ,
, 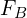 , and
, and 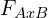
- These are the numbers which you use to determine if there is a main effect one
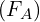 , main effect two
, main effect two 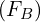 , and/or an interaction
, and/or an interaction 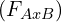 .
.
- Calculate
- Sixth Stage:
- If there is a significant main effect that has three or more levels, this is when you would conduct a post-hoc analysis for that factor alone. This would be no different than one done for a one-way ANOVA.
The conceptual meaning behind these calculations is that we’re dividing up the variance between the treatments so that we know the differences between the levels of factor A, the differences between the levels of factor B, and then the differences due to an interaction between the factors.
The assumptions of a two-factor ANOVA are as follows:
- The observations within each sample must be independent of each other.
- The populations from which the samples are selected must be normally distributed.
- The populations from which the samples are selected must have equal variances.
Effect Size
Once again we’re using partial eta squared, but this time we’re calculating it thrice – once for main effect one, once for main effect two, and once for an interaction. The formulas for these are relatively simple and can be found in the statistics formula glossary post.
This chapter was originally posted to the Math Support Center blog at the University of Baltimore on June 18, 2019.
