29 Introduction to Exponents and Polynomials
Jenna Lehmann
Evaluating Exponential Expressions
When working with exponents, it might be more helpful to think of them as multiple instances of multiplication. Some exponents are going to be more straight-forward, but be careful of the writing of some exponents.
Let’s take a look at some examples of evaluating exponential expressions:
In the expression below, this is an illustration of what we mean when we say that an exponent is like multiple multiplications. The exponents signify the number of times that the number 2 should be multiplied by itself.
![]()
In the next expression, the -3 is in parentheses. This means that the exponent outside of the parentheses needs to be applied to the number as a whole, including its being negative.
![]()
In this last expression, the exponent is sitting right next to the 3 without any parentheses holding the negative and the 3 together. In this case, think of it as though a -1 needs to be multiplied by 3 which is then multiplied by 3. No matter what the exponent is in this case, the answer will always be negative because a -1 is being multiplied to whatever number comes out of evaluating the exponent.
![]()
Using the Product Rule
When multiplying two or more of the same variable with exponents (meaning they have the same base number or letter), it’s as if you’re adding the exponents together. Below is a visualization of why that is. If we stretch out the expression so that each x is being multiplied by itself the proper number of times, it’s as if we added the 2 and 3 exponents to one another.
![]()
![]()
It’s important to remember, however, that you can only simplify expressions this way if the base number or variable is the same. In the example below, although it looks very complex, if we separate all numbers without exponents and all the different variables by type, we can easily achieve a simplified version of the expression.
![]()
So the answer is ![]()
Power of a Quotient Rule
The power of a quotient rule is that when a fraction exists within parentheses and is met with an exponent, everything within the parentheses is affected by the exponent. This includes any numbers which are attached to variables as well.
![]()
Quotient Rule for Exponents
If multiplying numbers with exponents is like adding the exponents together, then dividing is like subtracting the exponents.
![]()
![]()
Zero Exponent
For any number that has an exponent of 0, that number is always translated to 1. Try to keep this in mind as you start to deal with more complex equations involving exponents, as an equation can be better cleaned up by immediately translating a number or variable with an exponent of 0 to just be the number 1.
![]()
![]()
![]()
Negative Exponents
Negative exponents ask that the variable be flipped into (or sometimes out of) a fraction when translated. In the first example below, the x has to be flipped over into a denominator in order to get rid of the negative sign on its exponent. In the other, the x has to be flipped over to the numerator to get rid of the negative. In this case, however, the one in the denominator can be removed and the x no longer has to be part of a fraction.
![]()
![]()
Scientific Notation
Scientific notation is a process used to make either very big or small numbers easier to read. To translate a number into scientific notation, count the number of spaces it would take to get the first non-zero digit to become the one’s digit and then multiply that number by 10 to the number of digits moved. Here we can see an example. We have the number 0.000003. Simply start your pencil at the decimal and then create a bump around each 0 until you get to the other side of the number 3. Then, count the number of bumps. Remember that if you’re translating a big number to be smaller, the exponent next to the 10 should be positive. If you’re translating a small number to be bigger, the exponent next to the 10 should be negative.
![]()
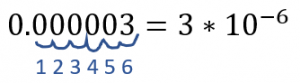
What is a Polynomial?
A polynomial is an equation which is created through the use of two or more algebraic terms. In the example below, each color represents a different term.
Polynomials can be made up of some or all of the following:
- Variables: the letters in the equation
- Constants: In the example above, the constant would be the 11. It’s a number that does not contain any modifiable variables.
- Exponents: These are the numbers that you’ll typically find attached to variables
- Addition, subtraction, multiplication, and division
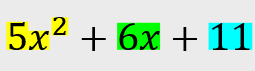
What isn’t Considered a Polynomial?
While a polynomial can appear in many different ways, there are some rules about what is not considered a polynomial. A polynomial is NOT:
An equation which contains division by a variable.
![]()
An equation that contains negative exponents.
![]()
An equation that contains fractional exponents.
![]()
An equation that contains radicals.
![]()
Evaluating Polynomials
Evaluating polynomials is just like solving any other math problem; make sure to use the order of operations. The order of operations is abbreviated to PEMDAS, which stands for Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction. To start, just plug the value for x or whatever letter you’re working with and then use the order of operations until you get your most simplified answer. Check out the example below:
- Evaluate
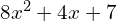 when
when 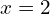
- Step 1: Substitute
- Step 2: PEMDAS
- Step 3: PEMDAS
- Step 4: PEMDAS
Adding Polynomials
When adding polynomials, keep in mind that you can only add together like terms. The like terms are highlighted in different colors in the example below. Don’t be intimidated by the parentheses when adding – just add like you normally would.
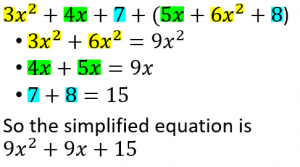
Subtracting Polynomials
Just like when adding polynomials, only like terms can be subtracted from one another. However, in this case, you do need to keep the parentheses in mind because of the minus side to the left of the second polynomial. Treat the minus sign like a -1, as if you were about to multiply everything in the parentheses by -1. This means that everything that was once positive will be negative and vice versa.
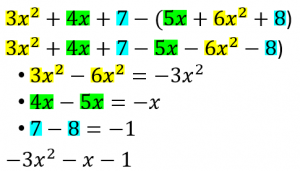
Polynomials with Two Variables
Don’t get distracted by the new variable! The rules from before still apply. Just be sure to separate each type of number by the base and then simplify.
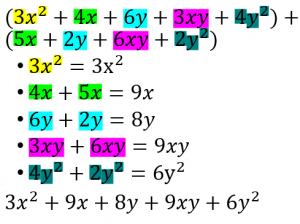
Multiplying Monomials
When working in equations that involve variables, multiplying two of the same variable results in an “addition” of exponents. For equations that simply have an “x” or “y,” imagine there’s a 1 exponent above it.
![]()
![]()
![]()
![]()
Multiplying Monomials by Polynomials
When multiplying monomials by polynomials, it’s important to multiply the monomial term by every term within the polynomial.

Using FOIL
When multiplying two different polynomials, remember to FOIL. First, multiply the two First variables in each polynomial. Then, multiply the Outside variables together. Next, multiply the Inside variables. Finally, multiply the Last variable of each polynomial.
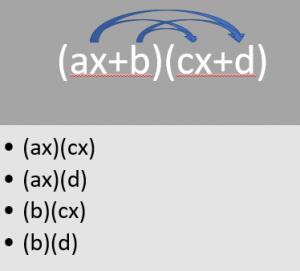
Multiplying Binomials
When multiplying binomials, it’s important to remember that each term of the first binomial should be multiplied with each term of the second.
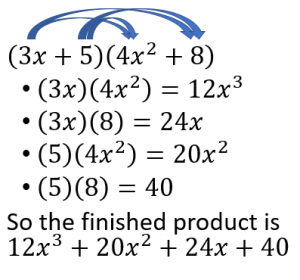
Multiplying Larger Polynomials
Don’t be intimidated by the added numbers. Just keep in mind that each variable needs to be multiplied by the other variables at some point. With larger polynomials like this one ![]() , I typically just go from left to right:
, I typically just go from left to right: ![]() .
.
Check out the example below.

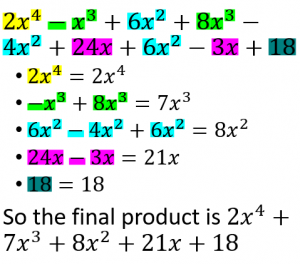
Dividing Polynomials by Monomials
Dividing a Polynomial by a Monomial of often easier when one breaks it up into smaller pieces.
![]()
Dividing a Polynomial by Another Polynomial
Solve ![]()
Step 1: Rewrite in descending powers and include missing variables (![]() )
)
![]()
Step 2: Long divide, asking yourself “what number multiplied by 2x would equal the number I’m focusing on?”
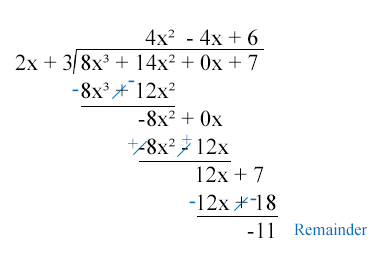
Step 3: Write the remainder out dividing it by the original polynomial
Thus, ![]()
This chapter was originally posted to the Math Support Center blog at the University of Baltimore on September 13, 2019.
