33 Mathematical Ideas: Basic Concepts of Set Theory

Symbols and Terminology

A set is a collection of objects of values that are in this case called elements or members. They can be described using words, lists, or set-builder notation.

• Words: a set of odd numbers less than 6
• Listing: {1,3,5}
• Set-builder notation: {x|x is an odd counting number less than 6}

If a set has no elements, it’s called an empty or null set and its symbol is Ø. Make sure not to write this as {Ø}, because that is technically incorrect.

It is important to make sure that a set is well-defined, meaning that there’s no room for subjective interpretation about whether something belongs in a set or not. An example of a well-defined set is a set of all numbers between 1 and 10. We can say for sure that 5 belongs and 13 doesn’t. A set that is not well defined is a set of all numbers that are aesthetically pleasing. It’s not clear what would define aesthetically pleasing so we’re unsure about whether 5 or 13 would fit.

The symbols ∈ and ∉ are used to describe whether something is or isn’t an element of a set. Going back to our example of all numbers between 1-10 (we’ll name this set A) we can say that 5 ∈ A while 13 ∉ A.

Important Definitions for Sets

Here are some important definitions before moving forward:

• Natural numbers or Counting numbers are all integers starting at 1: {1, 2, 3, 4,…}
• Whole numbers are all integers starting at 0: {0, 1, 2, 3, 4…}
• Integers are all whole numbers from -∞ to ∞: {… -3, -2, -1, 0, 1, 2, 3…}
• Rational numbers are numbers that can be created by dividing two integers (like 1/2 or 9/10 or 4/1).
• Real Numbers are any number that isn’t imaginary, so the typical integer, fraction, or decimal we’re used to. An imaginary number is when a negative number is square rooted (√-1)
• Irrational Numbers are decimals that can’t be expressed as the fraction of two integers. The square root of 2 would be an example of this because the decimals are ongoing and there is no discernible pattern to the decimals.
• A cardinal number is the number of elements in a set and it is written as n(A) and spoken as “n of A.” So if I was given set Z = {1, 5, 7, 2, 9, 10}, I would say n(Z) is 6.
• A finite set is a set that has a whole number as its cardinal number. So we could technically count how many elements are in a set.
• An infinite set is a set where the number of elements is infinite and we couldn’t possibly count them.
• Two sets are equal if two conditions are met: (1) every element of the first set is an element of the second set and (2) if every element of the second set is an element of the first one. That being said, it does not matter if the elements are written in a different order ({a, b, c, d} = {a, c, d, b}) and repeating elements doesn’t add a new element ({a, b, a, c, d, d} = {a, b, c, d}).

Venn Diagrams and Subsets

The universe in which we are working, or the area that we’re concerned within a set, is called the universal set. This consists of everything in the wider set. Venn diagrams are often used to discuss commonalities and differences between sets in the universal set. The universal set is everything within the rectangle encompassing the Venn diagram including the Venn diagram itself. The Venn diagram is made up of sets within U and can overlap. Set A is everything in circle A, set B is everything in circle B, and where they overlap are all the elements that they have in common.

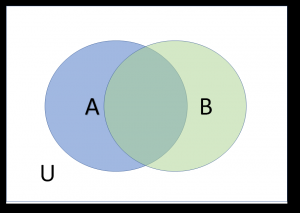
Complements of a set are everything that a set is not. The complement of A is A’ (spoken as A prime) and it includes everything in U except what is included in A.

Subsets of a Set

A subset is any set that is also part of another set. For example, if U = {1, 2, 3, 4, 5} and A = {1, 4, 5}, then we would say that A is a subset of U. This is denoted like this: A ⊆ U. If B = {1, 2, 4, 7}, because 7 is not part of U, we would say B is not a subset of U, also denoted like this: B ⊄ U.

There are different kinds of subsets. Any subset can be called a subset, but some can be described as a proper subset. A proper subset is a subset that has elements of a set but not exactly all of the elements in that set. For example, if set Y = {1, 2, 3} and Z = {1, 2, 3, 4}, then we could say that Y is a subset of Z and we could also say that Y is a proper subset of Z because it does not include all of the elements of Z. This is written as such: Y ⊂ Z.

Sometimes you will be asked to calculate how many subsets exist within a set. This can be calculated using powers of 2. For example, if I have the set {1, 4, 6, 2, 7}, I can see that there are 5 elements in the set. I make that 5 an exponent of 2 (2^5) to calculate how many subsets are possible: 32. To calculate the number of proper subsets, the equation is (2^n) – 1.

Set Operations

An intersection of sets is the elements of two sets that they have in common. For example, {1, 4, 5} ∩ {6, 9, 5} = {5}. Put in other words, A ∩ B = {x|x ∈ A and x ∈ B}. If two sets have no elements in common, they are called disjointed sets and written as such: A ∩ B = ø. A union of sets is the set of all elements belonging to either set one or set two, written as such: A ∪ B = {x|x ∈ A or x ∈ B}. A difference of sets is the set of all elements of the first set and not the second. For example, if set A is {1, 2, 3, 4, 5, 6} and B is {1, 3, 5}, then the difference would be {2, 4,6}. In other words, A – B = {x|x ∈ A and x ∉ B}.

When elements are placed in {braces}, it doesn’t matter in what order they are listed. When elements are placed in (parentheses), it’s called an ordered pair and it does matter what order they are listed in. In other words (a,b) ≠ (b,a). In the ordered pair (a,b), a is the first component and b is the second component.

A cartesian product of sets is a way of creating a set of ordered pairs. It’s written like A X B and when presented with a problem asking you to find cartesian products, you have to create ordered pairs with each number in each set in the order that the notation dictates. For example, if A = {1, 2, 3} and B = {8, 9}, and you were asked to find A X B, then the answer would be {(1,8), (1,9), (2,8), (2,9), (3,8), (3,9)}. If you were asked to find B X A, the answer would be {(8,1), (8,2), (8,3), (9,1), (9,2), (9,3)}. The cardinal number of a cartesian product is going to be the cardinal number of set 1 times the cardinal number of set 2, or n(A) x n(B).

This chapter was originally posted to the Math Support Center blog at the University of Baltimore on November 11, 2019.