Rational Expressions and Equations

Jenna Lehmann

31 Rational Expressions and Equations

Jenna Lehmann

What is a Rational Expression?

A rational number is a number that can be written as a quotient of integers. In other words, it’s any number that can create a nice and neat fraction. A rational expression is also a quotient, it’s just made up of polynomials. A rational expression can be written in the form P/Q. For example:

$\frac{2}{3}$ or $\frac{3y^8}{8}$ or $\frac{-4p}{p^3 + 2p + 1}$

Evaluating Rational Expressions

Rational expressions have different numerical values depending on what values replace the variables. For example:

$\frac{x + 4}{2x-3}$

If $x = 5$ then $\frac{5+4}{2(5)-3} = \frac{9}{10-3} = \frac{9}{7}$

If $x = 2$ then $\frac{2+4}{2(2)-3} = \frac{6}{4-3} = \frac{6}{1} = 6$

Identifying When a Rational Expression is Undefined

When the denominator of a rational expression is 0, then it is undefined. There are some equations in which the denominator is sometimes 0 and some in which the denominator is never 0. Take the following equation as an example.

$\frac{x}{x-3}$

When we set $x-3$ to equal 0, we find that when $x$ is 3, the denominator is 0. So when $x$ is 3, the rational expression is undefined.

$\frac{x^3-6x^2-10x}{3}$

The denominator of the above equation is never 0, and so it is never undefined.

Sometimes you will need to factor the denominator to find the variables which make it undefined, like in the following example.

$\frac{x^2+2}{x^2-3x+2}$

$x^2 - 3x + 2 = 0$

$(x - 2)(x - 1) = 0$

$(x - 2) = 0$ and $(x - 1) = 0$

So when $x$ equals 2 or 1, the expression is undefined.

Simplifying Rational Expressions

Sometimes a fraction made of polynomials can be simplified. This can be done by taking out the greatest common factor, like in the example below.

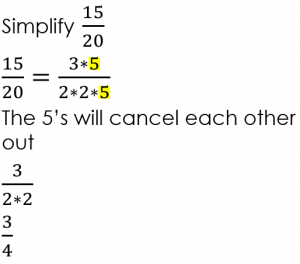
Example of simplifying rational expressions

This may also be done by factoring the polynomials in both the numerator and denominator.

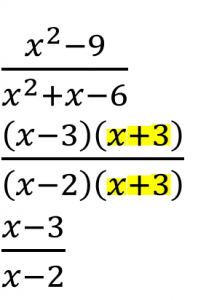
Example of simplifying rational expression with polynomials

Multiplying Rational Expressions

Multiplying rational expressions follow the same rules as multiplying other kinds of fractions. The numerator of one fraction is multiplied by the numerator of the other, and the denominator of one fraction is multiplied by the other.

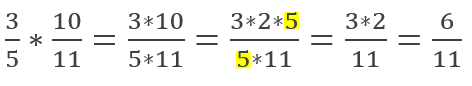
Example of multiplying rational expressions

This goes for polynomials as well. Just be sure to FOIL when necessary.

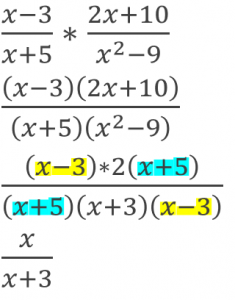
Example of multiplying a rational expression with polynomials

Dividing Rational Expressions

Remember that dividing fractions is the same thing as flipping the second fraction and multiplying.

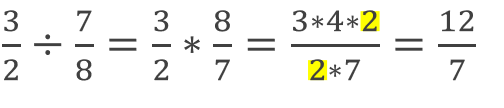
Example of dividing a rational expression

This is also true for polynomials. Again, don’t forget to FOIL when necessary.

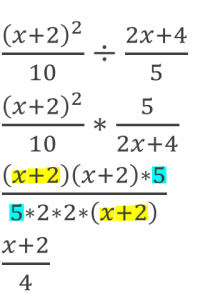
Example of dividing a rational expression with polynomials

Adding and Subtracting Rational Expressions with the Same Denominator

When adding and subtracting with rational expressions that have the same denominator, all you have to worry about is adding and subtracting what’s in the numerator.

$\frac{6}{5} + \frac{2}{5} = \frac{6+2}{5} = \frac{8}{5}$

This is true for any kind of term that may be in the numerator or denominator.

$\frac{5m}{2n} = \frac{m}{2n} = \frac{(5m+m)}{2n} = \frac{6m}{2n} = \frac{3m}{n}$

or

$\frac{2y}{2y-7} - \frac{7}{2y-7} = \frac{2y-7}{2y-7} = \frac{1}{1} = 1$

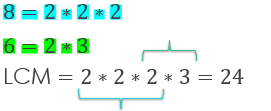
Finding the Least Common Denominator

Finding the least common denominator involves breaking each number up into its smallest variables and seeing how those numbers compare so that the smallest number that they both fit into appears. Take a look at the example below. 8 can be broken up into 2*2*2 and 6 can be broken up into 2*3. We need a number that satisfies the need for all of these numbers, even if a few overlap. The solution to this is 2*2*2*3. It incorporates the 8’s need to have 3 2’s and the 6’s need to have a 2 and a 3. 2*2*2*3 = 24 so our LCD is 24.

Sample equation with LCM

This also works with variables. We’re working with 5x and 15x^2. We need to find a number that fulfills the need of a 5 and an x as well as a 5, a 3, and 2 x’s. The equation 5*x*x*3 fulfills all of those needs. So our LCD is 15x^2.

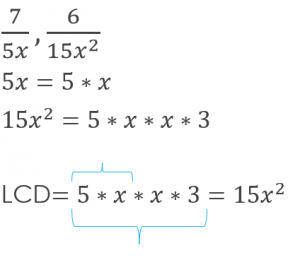
Sample variables equation with LCD

Writing Equivalent Rational Expressions

When writing equivalent rational expressions, we are, in a sense, multiplying an expression of 1.

$\frac{P}{Q} = \frac{P}{Q} \ast 1 = \frac{P}{Q} \ast \frac{R}{R} = \frac{PR}{QR}$

This is useful for when we want to translate one equation to keep the same value but use a different denominator.

In this case, we have to ask ourselves, “what can I multiply by $9a$ in order to get $27a^2b$ ?”

$\frac{4b}{9a} = \frac{?}{27a^2b}$

$\frac{4b}{9a} \ast \frac{3ab}{3ab} = \frac{12ab^2}{27a^2b}$

Adding and Subtracting Rational Expressions with Different Denominators

Find the LCD and then multiply one rational expression by what’s missing from it to get that LCD in the denominator. Make sure to do this with the other fraction, if necessary, so that in the end, both fractions have the same denominator – the LCD.

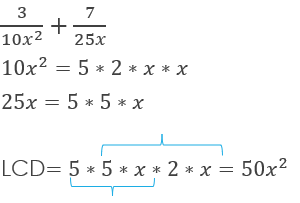
Example rational expression with LCD

$\frac{3}{10x^2} = \frac{7}{25x} = \frac{3(5)}{10x^2(5)} + \frac{7(2x)}{25x(2x)}$

$\frac{15}{50x^2} + \frac{14x}{50x^2} = \frac{15+14x}{50x^2}$

Solving Equations Containing Rational Expressions

Sometimes, you will be asked to solve for a missing variable when there are equations containing rational expressions. I recommend doing what is needed so that the denominators of all the numbers are eliminated and you can work with whole numbers again.

$\frac{x}{2} + \frac{8}{3} = \frac{1}{6}$