19 Independent t-tests
Jenna Lehmann
We have talked about single sample t-tests, which is a way of comparing the mean of a population with the mean of a sample to look for a difference. With two-sample t-tests, we are now trying to find a difference between two different sample means. More specifically, independent t-tests involve comparing the means of two samples which are distinctly different from one another in regards to the individuals within each sample. For example, a group of pet owners vs. a group of folks who don’t own pets. These two groups are completely independent of one another. This distinction will be important in a later post.
A more technical explanation of the difference between a single sample and two-sample is that a single sample t-test revolves around drawing conclusions about a treated population based on a sample mean and an untreated population mean (no standard deviation). An independent sample t-tests are all about comparing the means of two samples (usually a control group/untreated group and a treated group) to draw inferences about how there might be differences between those two groups in the broader population
There are some distinct advantages and disadvantages to this approach when compared to other approaches. To avoid confusion, we won’t describe the other approaches here but will just mark the advantages and disadvantages of this one here for your consideration:
Advantages:
- Gives the opportunity to conduct an experiment with very little contamination by extraneous factors.
- Lowers the chance of participants suffering from boredom after a long series of tests as well as skewing the results by becoming more accomplished through practice experience.
Disadvantages:
- Can be complex.
- Requires a large number of participants.
- Needs a new group for every treatment and manipulation.
- Confounding variables brought in by the individuals in the study can weaken results.
Hypothesis Testing with Independent t-tests
The null and alternative hypotheses for this kind of test are as follows:
![]() (no difference in the population means)
(no difference in the population means)
![]() (there is a mean difference)
(there is a mean difference)
Steps of calculating an independent samples t-test (from this point forward, if there is a larger formula you’re looking for, see our formula guide glossary):
- Calculate the estimated standard error by calculating pooled variance and figuring out the degrees of freedom for each group.
- Subtract the two means from one another (we assume that the difference between the population means will be 0 given the null hypothesis) and then divide by the standard error.
- Determine the critical region based on your alpha level and whether you’re running a one or two-tailed test. Then decide whether your calculated t-test falls within the critical region or not.
- Make a decision about the null hypothesis based on this comparison.
Assumptions of independent sample t-tests:
- The observations within each sample must be independent.
- The two populations from which the samples are selected must be normal.
- To justify using the pooled variance, the two populations from which the samples are selected must have equal variances (homogeneity of variance); essentially the standard deviation of after treatment should be very similar to the standard deviation presented before treatment. This can be confirmed using SPSS or Excel. This can also be done using Hartley’s F-max test, which is described later on in this chapter.
Estimated Standard Error and Pooled Variance
To calculate the estimated standard error, you need to first calculate pooled variance, especially because not all treatment or non-treatment groups will have the same number of scores, and so you need to weight in both groups before coming to terms with the overall estimated standard error. Remember that the estimated standard error is how we calculate the standard error when there’s no population mean to go off of.
In essence, the steps for calculating a t-test by hand are:
- Find the sum of squares of each sample.
- Calculate the pooled variance given the sums of squares you just found and the degrees of freedom (
 for each sample).
for each sample). - Calculate the estimated standard error using that pooled variance.
- Plug the estimated standard error into the t-test formula and solve for
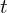 .
.
Effect Size of Independent Samples t-test
We use Cohen’s d to get effect size. For this particular test, it’s mean 1 minus mean 2 all divided by the square root of the pool variance calculated earlier. In this case, instead of comparing the effects of a sample to the population (asking, is this practically significant rather than just statistically significant?), we’re comparing the effects of two different samples.
Hartley’s F-Max Test
Hartley’s F-max test is a statistical test to evaluate the homogeneity assumption. To compute, you need to compute the sample variance of each sample individually. Then, you need to make a fraction with the biggest variance on top and the smallest one on the bottom. Finally, compute. The F-max value computed for the sample data is compared with the critical value found in an F-max table. If the sample value is larger than the table value, then you can conclude that the homogeneity assumption is not valid.
If you’re looking for more help on learning the concept of the independent samples t-test or how to calculate it, check out this series of videos (each one about five minutes long):
This chapter was originally posted to the Math Support Center blog at the University of Baltimore on June 11, 2019.
