20 Repeated Measures t-test

A repeated measures or paired samples design is all about minimizing confounding variables like participant characteristics by either using the same person in multiple levels of a factor or pairing participants up in each group based on similar characteristics or relationship and then having them take part in different treatments. Matched subjects is another word used to describe this kind of test and it is used specifically to refer to designs in which different people are matched up by their characteristics. Participants are often matched by age, gender, race, socioeconomic status, or other demographic features, but can also be matched up on other characteristics the researchers might consider possible confounds. Twin studies are a good example of this kind of design; one twin has to be matched up with the other – they can’t be matched to someone else’s twin.

To reiterate the differences between a repeated measures t-test and the other kinds of tests you may have learned up to this point, a single sample t-test revolves around drawing conclusions about a treated population based on a sample mean and an untreated population mean (no standard deviation). An independent sample t-tests are all about comparing the means of two samples (usually a control group/untreated group and a treated group) to draw inferences about how there might be differences between those two groups in the broader population. Different, randomly assigned participants are used in each group. Related samples t-tests are like independent sample t-tests except they use the same person for multiple test groups or they match people based on their characteristics or relationships to cut down on extraneous variables which may interfere with the data.

Mean Difference and Estimated Standard Error of the Mean Difference

The mean difference is calculated by subtracting the two scores collected from each person (because there are two testing groups), adding all of those differences up, and then dividing that number by the number of scores. This is done because rather than just compare means between the two samples, like in an independent samples t-test, we have the opportunity to first calculate the difference between each individual to see how the treatment affected them.

The estimated standard error of the mean difference is a measure of how much the mean difference might vary from one occasion to the next. This is different from independent measures because instead of pooling variance between two samples, you base your sum of squares on the difference between the two scores and then calculate the estimated standard error like you would a single sample t test.

Hypothesis Testing with Repeated Measures t-tests

The null and alternative hypothesis are written as follows:

or that there is no difference between the two conditions

or that there is a significant difference between the two conditions

Steps for calculating a repeated measures t-test (all formulas needed can be found in the statistics formula glossary):

1. State the null and alternative hypothesis
2. Locate the critical region (remember that the 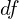is )
3. Calculate the t statistic using the t formula after calculating the estimated standard error of the mean difference.
4. Make a decision.

Once again, there are some advantages and disadvantages to using this approach.

Advantages:

• Fewer subjects needed
• Is well-suited for studying changes over time (developmental, learning, studying)
• Reduces or eliminates caused by individual differences within the participants by either linking participants up based on characteristics or by using the same person twice.

Disadvantages:

• Increases the likelihood that outside factors that change over time may be responsible for changes in the participants’ scores.
• Participation in the first treatment could affect scores in the second treatment (practice, fatigue, etc.).

Effect Size for Repeated Measures t-tests

Once again, Cohen’s d is the effect size measurement of choice. In this case, it’s the sample mean difference over the sample mean deviation (so whatever you found as the variance, square root that to get the sample mean deviation).

Variability as a Measure of Consistency

If a treatment consistently adds a few points to each individual’s score, then the set of difference scores are clustered together on a normal distribution curve with relatively small variability. In this situation, with small variability, it is easy to see the treatment effect and it is likely to be significant. High variability means that there’s no consistency with a treatment effect, meaning that it’s harder to see that there’s any difference between groups and it’s unlikely that a significant difference will be found.

Degrees of Freedom

Before, when we were working with independent t-tests, the degrees of freedom was for each sample, so in the end, it was . However, for a repeated measures t-test, we’re only needing degrees of freedom for the mean difference. Therefore, the total degrees of freedom is simply .

This chapter was originally posted to the Math Support Center blog at the University of Baltimore on June 11, 2019.