30 Factoring Polynomials
Jenna Lehmann
Finding the Greatest Common Factor (GCF)
Finding the greatest common factor simply involves finding the largest number or term which will fit evenly into each number or term in a list. The way I like to go about this is by breaking each number or term into its smallest parts. Break each number down until you are multiplying together only prime numbers. All the numbers that they have in common should then be multiplied back up to create the GCF.
This is what it would look like in a list of numbers:
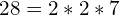
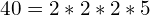
- The greatest common factor is
 .
.
And this is what it would look like in a list of terms:
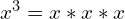
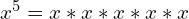
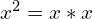
- The greatest common factor is
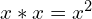
Sometimes, you will have to factor out the GCF in a function. In this case, treat each term like an individual and follow the instructions mentioned above. Then, whatever the GCF is, divide each term by that GCF, rewrite the function, and make sure to place the GCF outside of a parenthesis which contains the new function.

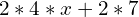
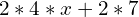 ; 2 is the greatest common factor
; 2 is the greatest common factor
- The final answer is
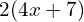
Factoring by Grouping
- Step 1: Group the terms in two groups of two terms so that each group has a common factor.
- Step 2: Factor out the GCF from each group.
- Step 3: If there is a common binomial factor, factor it out.
- Step 4: If not, rearrange the terms and try these steps again.
- Step 5: Make sure to check your work by multiplying (FOIL-ing) your answer to see if you can get back to the original problem.
![]()
![]()
Factoring Trinomials of the Form 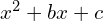
Sometimes trinomials can be factored into two binomials. It helps to make a chart in order to find the correct pairs of numbers. The pairs of numbers to go into (x+_)(x+_) depend on whether the sum of a pair of factors for the third term is equal to the number presented in the second term.
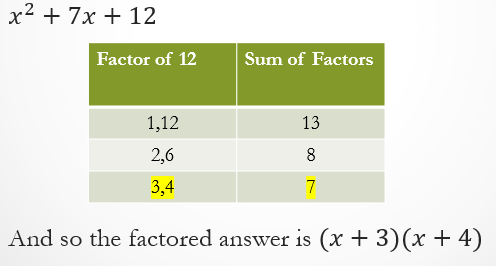
Factoring Trinomials of the Form 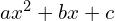
Step 1: Split the first term to ![]() and
and ![]() .
.
Step 2: Find all possible factors of the third term.
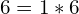 or
or 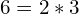
Step 3: Test Factors. This first one creates the wrong middle number.
This one also doesn’t work. Just keep testing. Sometimes, you will try everything and it still doesn’t quite work. Try splitting ax differently. In this case, 3 can only be split into 3 and 1, but if you’re working with 6, for example, you could try splitting it into 6 and 1 or 2 and 3.
Step 4: Finally, this set works. Make sure to check your work by FOIL-ing.
Factoring Out the GCF with Polynomials
Sometimes before we can even begin to factor a polynomial, we have the ability to factor out a common factor of all 3 terms. In the example below, notice all the numbers have a GCF of ![]() , we can start by factoring it out.
, we can start by factoring it out.
![]()
![]()
From there, we can continue to factor as we normally would.
![]()
Factoring Trinomials of the Form 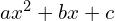 by Grouping
by Grouping
We can also use the grouping method for trinomials. Take the example problem below.
![]()
We can rewrite this so that there is an even number of terms, as shown here:
![]()
We want to find a factor of 24 (because 2 from the first term multiplied by 12 of the third term) that also adds up to 11.

![]()
Now that we have our middle numbers, we can group.
![]()
Now we’ll factor out the greatest common factors within each group. It looks like we have a common binomial in each group.
![]()
So our end product is:
![]()
Factoring Perfect Square Trinomials and the Difference of Two Squares
Decide whether ![]() is a perfect square trinomial
is a perfect square trinomial
Two terms ![]() and
and ![]() are squares
are squares ![]()
Twice the product of ![]() and
and ![]() is the final term of the trinomial
is the final term of the trinomial ![]()
Thus, ![]() is a perfect square trinomial
is a perfect square trinomial
This means that it can easily be factored to ![]()
Factoring the Difference of Two Squares
When both terms in a binomial are squares (meaning that they are a variable which includes a square or a number which can be evenly square-rooted) and the signs of the terms are different, one can use the following equation to factor it:
![]()
For example, ![]()
![]()
![]()
Solving Quadratic Equations by Factoring
Factoring can also be used to solve quadratic equations, like so:
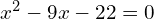
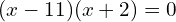
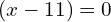 , and so
, and so 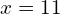
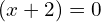 , and so
, and so 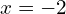
So the solutions to this quadratic equation are 11 and -2.
If the equation has a degree greater than two, it can be solved by factoring and then using the method above.
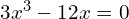
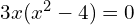
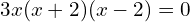
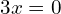 , means
, means 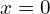
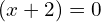 , means
, means 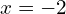
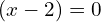 , means
, means 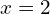
So the solutions are 0, 2, and -2.
This chapter was originally posted to the Math Support Center blog at the University of Baltimore on September 25, 2019.
