Spatial Analysis and Mapping with R
2 Coordinate Reference Systems
When working with spatial data, coordinate reference systems (CRS) are a key component. CRS allow to determine positions on a three-dimensional surface (usually Earth) and project them onto a two-dimensional surface (“flattening”). Key components that define a CRS are:
- Coordinate system: A
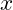 and
and 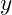 and
and 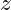 grid that defines where the data points are located in space.
grid that defines where the data points are located in space. - Units: Units of the distances on the
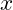 and
and 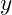 axis of the grid (horizontal unit) and the
axis of the grid (horizontal unit) and the 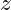 axis (vertical unit)
axis (vertical unit) - Datum: Model of the shape of the object (in our case, Earth), that defines the origin of the coordinate system (or, the reference point). For a global system for example the reference point is the Prime Meridian and the Equator.
- Projection: The mathematical equation used to project positions on the 3D object onto a 2D flat surface.
2.1 Geographic and Projected CRS
Geographic Coordinate Reference Systems are used to map places on the surface of a globe (i.e., Earth) based on two values, longitude and latitude. Longitude is the location in East-West direction in angular distance (usually degrees) from the Prime Meridian. Latitude is the North/South location in angular distance from the Equator. Units of angular distances are not linear. Therefore, geographic CRS are not suitable to calculate and compare distances between locations.
Most geographic CRS model the Earth as an ellipsoid rather than a perfect sphere. What ellipsoid is used is defined by the datum.
There are two types of datum: a geocentric datum and a local datum. The geocentric (or geoid) datum (such as the WGS84) uses the Earth’s center of gravity as its center. The ellipsoid is not optimized for local variations. A local datum, such as the North America Datum (NAD) optimize the ellipsoid to include local variations such as large mountain ranges.
Projected Coordinate Reference Systems are based on a Cartesian coordinate system on a flat surface. Map projections are used to convert the 3D surface of the Earth into ![]() and
and ![]() coordinates of the projected
coordinates of the projected CRS. Projections are grouped into 3 main types, conic, cylindrical, and planar.
2.2 Formats of CRS Definitions
There are multiple formats that define CRS, including WKT (well-known text) strings, proj4string, and EPSG.
Spatial packages in R support two ways of describing CRS: EPSG code and proj4string definitions. EPSG code defines one specific CRS whereas proj4string definitions are more flexible and allow to define projection, datum etc.
2.3 Common CRS
The World Geodetic System 1984 (WGS84or WGS 84) and the North American Datum 1983 (NAD83) are two commonly used CRS in the U.S. Both systems are geocentric and use Greenwich as the Prime Meridian. Units of measurements are degrees, and the axes longitude (![]() ) and latitude (
) and latitude (![]() ).
).
The EPSG code of the WGS 84 is 4326, and the proj4string is +proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs. WGS 84 is used by the global positioning system (GPS).
The NAD83 is a local datum used in Canada and the U.S. The EPSG of the latest rendition of NAD83 (2011) is 4269 and the proj4string is +proj=longlat +ellps=GRS80 +datum=NAD83 +no_defs. It uses a different ellipsoid model (GRS80). Furthermore, NAD83 coordinates for points on North American Plate do not change over time. Thus, coordinates of locations on the North American Plate are not affected by plate tectonics. Having said that, position west of the San Andreas Fault and Hawaii are not on the North American Plate. In contrast, WGS 84 position coordinates are defined based on the average of stations around the globe. Therefore coordinates of WGS 84 defined positions deviate by 1 to 2 cm per year from coordinates established by NAD83. Today the deviations are large enough that they need to be taken into consideration.
If calculations of area or distance are required, and to avoid distortions, spatial data using a geocentric CRS need to be re-projected to a projected CRS with linear units (meter, feet, US survey feet). Which projected CRS to use depends on the region. For Maryland, NAD83(2011)/Maryland (EPSG: 6487, unit: meter; or EPSG: 6488, unit: US survey feet) are often used.
Note, there are (at least) two other EPSG codes that seem to be equivalent to EPSG:6487 and EPSG:6488, namely EPSG:26985 and EPSG:2248.
proj4stringofEPSG:6487and26985:EPSG:6487:
+proj=lcc +lat_0=37.6666666666667 +lon_0=-77 +lat_1=39.45 +lat_2=38.3 +x_0=400000 +y_0=0 +ellps=GRS80 +units=m +no_defs.EPSG:26985:
+proj=lcc +lat_0=37.6666666666667 +lon_0=-77 +lat_1=39.45 +lat_2=38.3 +x_0=400000 +y_0=0 +datum=NAD83 +units=m +no_defs.
proj4stringofEPSG:6488and2248:EPSG:6488:
+proj=lcc +lat_0=37.6666666666667 +lon_0=-77 +lat_1=39.45 +lat_2=38.3 +x_0=399999.9998984 +y_0=0 +ellps=GRS80 +units=us-ft +no_defs.EPSG:2248:
+proj=lcc +lat_0=37.6666666666667 +lon_0=-77 +lat_1=39.45 +lat_2=38.3 +x_0=399999.9998984 +y_0=0 +datum=NAD83 +units=us-ft +no_defs.
EPSG:6487 and 6488 were released by the U.S. National Geodetic Survey (Revision date: 2013-10-09). The area covered is Maryland (IOGP Geomatics Committee, 2021). EPGS:26985 and 2248 were released by the U.S. Defense Agency TR8350.2 (Revision date: 2014-11-19). The area covered appears to be much broader (WGS 84 bounds: -172.54 23.81; -47.74 86.46) (MapTiler Team, 2019). These two EPSG are not included in the EPSG Geodeditc parameter dataset (v10.018).
For both, EPSG:6487 and EPSG:6488 the latitude/longitude at the (artificial) origin (0, 0) is 37°34’38.14264″N and 81°31’45.07877″W. False Easting at the 77th meridian is 400,000 m (EPSG:6487) and 399,999.9998984 m (EPSG:6488) (Reger, 2013).
References
IOGP Geomatics Committee (2021). EPSG Geodetic Parameter Dataset. Retrieved April 5, 2021, from https://epsg.org/home.html
MapTiler Team (2019). epsg.io, Coordinate Systems Worldwide. Retrieved April 5, 2021, from https://epsg.io
Reger, J. P. (2013). Maryland Geological Survey: A user’s guide to Maryland coordinate system. Retrieved April 6, 2021, from http://www.mgs.md.gov/geology/maryland_coordinate_system.html
